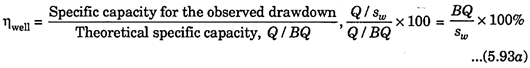ADVERTISEMENTS:
The specific capacity (Q/sw) of a well is the discharge per unit drawdown in the well and is usually expressed in lpm/m. This is a measure of the effectiveness of a well. From Eqs. (4.78), (5.89) and (5.90).
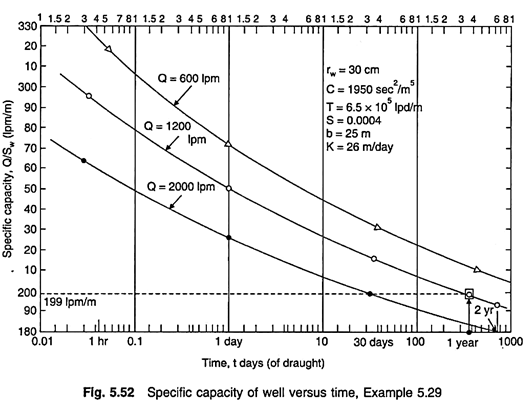
Which shows that the specific capacity of a well is not constant but decreases with the increase in pumping rate (Q) and prolonged pumping (t) (Fig. 5.52). The probable drawdown for an unconfined aquifer may be obtained from [by putting R ≈ 300 rw and rw ≈ 15 cm in Eq. (5.5)]
Q/sw = T/1.2
And for a confined aquifer [by putting R ≈ 3000 m and rw ≈ 15 cm in Eq. (5.7)]
Q/sw ≈ T/1.6
On an average Q/sw = T/1.4 …(5.93)
If the well is small in diameter and is pumped at a higher rate, the friction losses will increase. The maximum safe yield of a well or well field is the capacity of the aquifer to supply water without causing a continuous lowering of the water table or piezometric surface and is, therefore, limited by the rate at which the ground water is replenished by rainfall.
ADVERTISEMENTS:
Excessive lowering of the ground water table by pumping may result in crop failures, depletion of a nearby stream by increased percolation losses, salt water intrusion in coastal aquifers, and occasionally serious settlement of the ground surface.
Also from Eqs. (5.5) and (5.7), Q is inversely proportional to log10 R/rw. The percentage increase in discharge for the increase in diameter is given in Table 5.21 and illustrates the fallacy of the idea that big wells necessarily mean proportionately large yields.
Well Efficiency:
The efficiency of a well, for a specified duration of pumping, is given by-
Example 1:
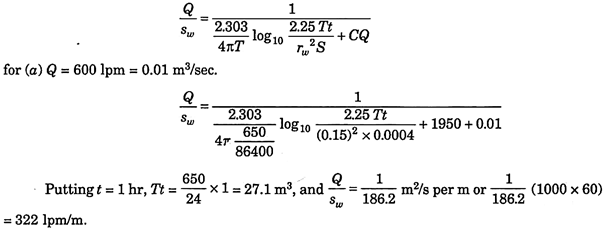
A 30 cm well penetrates fully an infinite non-leaky artesian aquifer having T = 6.5 × 105 lpd/m, S = 0.0004. Construct specific capacity curves for the well for t = 1 hr, 1 day, 1 month, 1 year and 2 years of draught, when the well is pumped at the rate of- (a) 600 1pm, (b) 1200 1pm, and (c) 2000 1pm. Assume a well loss coefficient of 1950 sec2/m5. What is the drawdown in the well after pumping for one year at the rate of 1200 1pm?
Solution:
The specific capacity of the well, Eq. (5.92):
Similarly, putting t = 1 day, 1 month (30 days), 1 year (365 days), and 2 years (730 days), the specific capacities are computed as 273, 234.5, 212, and 207 1pm/m, respectively. Similarly for (b) Q = 1200 1pm = 0.02 m3/sec, and t = 1 hr, 1 day, 1 month, 1 year and 2 years, the specific capacities are computed as 292, 251,218,199 and 194 1pm/m, respectively, and for (c) Q = 2000 1pm = 0.0333 m3/sec, and t = 1 hr, 1 day, 1 month, 1 year and 2 years, the specific capacities are computed as 259, 226, 199, 183, and 179 1pm/m, respectively.
The specific capacity curves are thus constructed as shown in Fig. 5.52. For Q = 1200 1pm, t = 1 year, Q/sw = 199 1pm/m.
Therefore, drawdown in the well at the end of 1 year,
ADVERTISEMENTS:
sw = 1200/199 = 6.03 m
Thus, the specific capacity is a useful concept and indicates the productivity of both aquifer and well in a single parameter. A high specific capacity indicates an efficient (well-constructed and developed) good yielding well. A decline in specific capacity may indicate failure of well screens (by clogging or so) or declining S or T values due to declining water table or piezometric surfaces. Specific capacity decreases faster in unconfined aquifers since the decline of the water table reduces T.
Graphical trial-and-error procedure of Rorabaugh (1953) to determine well losses from the step-drawdown test data:
Example 2:
The following discharge drawdown data are obtained from a production well in a step-drawdown test:
Determine the coefficients of formation loss and well loss. Comment on the specific capacity values you obtain.
Solution:
Which shows that a plot of’ (sw/Q = B) vs. Q’ on log-log paper should yield a straight line whose slope m = n 1, and when Q = 1, C = sw/Q = B. Values of B are tried till a straight line relation plot is obtained Fig. 5.53.
When Q = 1, sw/Q – B – 0.44 = C, min2/m5
Which is < 0.5; hence the production well is properly designed and developed.
Further,
It may be noted that the well loss increases with Q rapidly, and in the last case, it is as high as 2.78/3.75 × 100 = 74%, since ‘n’ usually lies between 2 and 3.
Since the well loss varies as the nth power of the entrance velocity, the well loss can be kept down by increasing rw. The step-drawdown test shows how much head is lost in the aquifer and how much in and around the well (screen and gravel pack). Excessive well losses indicate improper design and development of the well or deterioration of the screen. Also the value of B obtained from the test can be used to estimate T of the aquifer, using the appropriate well flow equation relating the formation loss to Q. The specific capacity decreases with increasing Q.
Example 3:
A 30 cm well penetrates completely an infinite non-leaky artesian aquifer having T = 600 m2/day, 8 = 0.0004. The well is continuously pumped at the rate of 60 m3/hr. Assuming a well loss coefficient of 0.5 min2/m5, and index n = 2.3, determine the specific capacity and the drawdown in the pumping well after 1 year of drought. What is the well efficiency?
Solution:
Substituting the given data, after t = 1 year,