Measuring the Average Depth of Rainfall: 3 Methods | Atmosphere | Geography

For any time duration, the average depth of rainfall falling over a catchment can be found by the following three methods: 1. The Arithmetic Mean Method 2. The Thiessen Polygon Method 3. The Isohyetal Method.

1. The Arithmetic Mean Method:

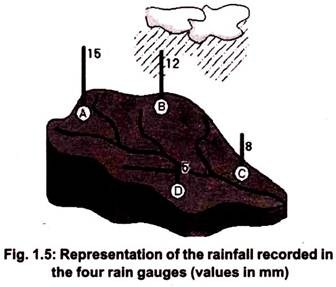
The simplest of all is the Arithmetic Mean Method, which taken an average of all the rainfall depths as shown in Fig. 1.5.

Average rainfall as the arithmetic mean of all the records of the four rain gauges, as shown below:

Average rainfall = (5 + 8 + 12 + 15)/4 = 10.0 mm.

2. The Thiessen Polygon Method:

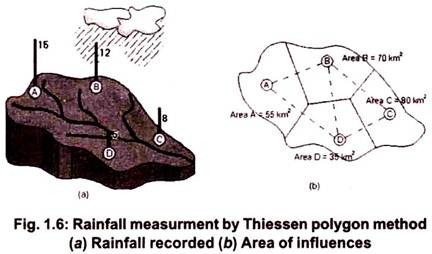
This method, first proposed by Thiessen in 1911, considers the representative area for each rain gauge. These could also be thought of as the areas of influence of each rain gauge, as shown in Figure 1.6.

These areas are found out using a method consisting of the following three steps:

a. Joining the rain gauge station locations by straight lines to form triangles.

b. Bisecting the edges of the triangles to form the so-called “Thiessen polygons”.  

c. Calculate the area enclosed around each rain gauge station bounded by the polygon edges (and the catchment boundary, wherever appropriate) to find the area of influence corresponding to the rain gauge.

For the given example, the “weighted” average rainfall over the catchment is determined as:

3. The Isohyetal Method:

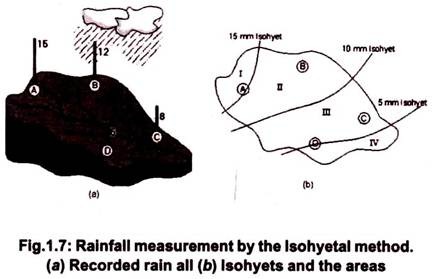
This is considered as one of the most accurate methods, but it is dependent on the skill and experience of the analyst. The method requires the plotting of isohyets as shown in the figure and calculating the areas enclosed either between the isohyets or between an isohyet and the catchment boundary. The areas may be measured with a planimeterif the catchment map is drawn to a scale.

For the problem shown in Fig. 1.7, the following may be assumed to be the areas enclosed between two consecutive isohyets and are calculated as under:

Area I = 40 km²

Area II = 80 km²

Area III = 70 km²

Area IV = 50 km²

Total catchment area = 240 km²

The areas II and III fall between two isohyets each.

Hence, these areas may be thought of as corresponding to the following rainfall depths:

Area II: Corresponds to (10 + 15)/2 = 12.5 mm rainfall depth

Area III: Corresponds to (5 + 10)/2 = 7.5 mm rainfall depth

For Area I, we would expect rainfall to be more than 15 mm but since there is no record, a rainfall depth of 15mm is accepted. Similarly, for Area IV, a rainfall depth of 5 mm has to be taken.

Hence, the average precipitation by the isohyetal method is calculated to be:

Note Isohyets:

Lines drawn on a map passing through places having equal amount of rainfall recorded during the same period at these places (these lines are drawn after giving consideration to the topography of the region).

Planimeter:

This is a drafting instrument used to measure the area of a graphically represented planar region.