ADVERTISEMENTS:
In this article we will discuss about the optical and physical properties of minerals.
Physical Properties of Minerals:
1. Colour:
The colour of any object is a light dependent property- it is the appearance of the particular object in light (darkness destroys colour). A particular colour is produced by reflection of some and absorption of other components of white light. A mineral shows colour of that wavelength of the white light which is not absorbed by it by virtue of its composition and atomic structure.
ADVERTISEMENTS:
In nature, minerals of all perceivable colours are known to occur. Quite a few common minerals generally occur in characteristics colours so that they can be easily identified from their colours.
On the basis of colour, a mineral may belong to any one of the three types:
(i) Idiochromatic having a characteristic, fairly constant colour related primarily to the composition of mineral. Metallic minerals (e.g. of copper group) belong to this category.
(ii) Allochromatic having a variable colour; the variety in colour is generally due to minute quantities of colouring impurities thoroughly dispersed in the mineral composition. Many non-metallic minerals like quartz, calcite, fluorite and tourmaline etc. may occur in more than two colours depending on the nature of impurities.
(iii) Pseudochromatic showing a false colour. Such an effect generally happens when a mineral is rotated in hand; it is then seen to show a set of colours in succession. This change or play of colours is attributed to simultaneous reflection and refraction from the mineral surface due to minute inclusions of impurities in the mineral at different locations.
ADVERTISEMENTS:
Some of the peculiar phenomena connected with colour in minerals are briefly explained below:
i. Play of Colours:
It is the development of a series of prismatic colours shown by some minerals on turning about in light. The colours change in rapid succession on rotation and their effect is quite brilliant and appealing to the eye. These are caused by the interference of light reflected from numerous cleavage surfaces of the mineral. Example- diamond.
ADVERTISEMENTS:
ii. Change of Colours:
It is similar to play of colours except that the rate of change of colours on rotation and their intensity is rather low. Each colour continues over a larger space in the mineral before the other takes over. Example- labradorite.
iii. Iridescence:
Some minerals show rainbow colours (similar to those appearing in drops of oil spilled over water) either in their interior or on the exterior surface. This is called iridescence. It is also related to reflections from inclusions. Example- Limonite and hematite.
iv. Tarnish:
This may be described as a phenomenon of change of original colours of a mineral to some secondary colours at its surface due to its oxidation at the surface. Some minerals tarnish very quickly so that their exterior colour is quite different from the interior colour. Example- Bornite and Chalcopyrite.
Although colour is never taken as a diagnostic or conclusive property in the final identification of minerals, it is invariably studied first of all and is generally very helpful. In fact, some minerals have typical colours associated with them such as- Lazurite (deep blue), Pyrite (brass yellow), Cinnabar (carmine red), magnetite (black) and so on. Quite a few minerals may be colourless and transparent when absolutely pure, e.g. quartz, calcite, diamond and gypsum.
2. Lustre:
Simply defined, it is the shine of a mineral.
Technically speaking, it is intensity of reflection of light from the mineral surface and depends at least on three factors:
ADVERTISEMENTS:
(i) The refractive index of the mineral.
(ii) The absorption (of light) capacity of the mineral.
(iii) The nature of reflecting surface.
The same mineral may show a poor lustre on rough surface and brilliant lustre on a cleavage face.
Broadly speaking, lustre may be classified into metallic and non-metallic types. Metallic lustres are characteristic of high density, high refractive index and opaque minerals like galena, pyrite and chalcopyrite.
In the non-metallic luster the reflection may vary from very brilliant shine as that of diamonds to very feeble greasy luster of olivine and nepheline.
While studying lustre of the minerals, one may make use of following qualitative terms:
(i) Metallic- shine resembles to known metals; example- galena
(ii) Adamantine- luster of diamonds; very brilliant; example- diamond
(iii) Vitreous- shine typical of glass, ice etc.; example- quartz
(iv) Pearly- resembling shine of pearls; example- labradorite
(v) Silky- like the shine of pure silk; example- gypsum
(vi) Resinous- shine is oily, waxy or greasy; example- nepheline.
(vii) Dull or earthy, where shine is almost absent because no light is reflected due to highly porous nature of the mineral; example- chalk, clay, bauxite.
It may be mentioned that lustre is entirely independent of colour of the mineral. A deeply coloured mineral may be lusterless and vice versa.
3. Streak:
It is an important and diagnostic property of many coloured minerals. Simply defined, streak is the colour of the finely powdered mineral as obtained by scratching or rubbing the mineral over a rough unglazed porcelain plate. The plate is often named as a streak plate in a geology laboratory.
Colourless and transparent minerals will always give a colourless streak that has no significance. The coloured and opaque minerals, especially of ore groups, give typically characteristic streaks quite different from other similarly looking minerals. For instance, chromite and magnetite resemble closely in their other physical properties- both are almost black. These may be at once distinguished by their streaks: brown for chromite and black for magnetite.
It follows that the colour of a mineral may or may not be the same as its streak. For identification, streak is relied upon more than the colour of the mineral.
4. Hardness:
It is a fairly constant and diagnostic property of minerals. Hardness may be defined as the resistance, which a mineral offers to an external deformation action such as scratching, abrasion, rubbing or indentation. Hardness of a mineral depends on its chemical composition and atomic constitution.
Broadly speaking hardness of minerals as determined conventionally is a qualitative property determined in relative terms. It was in 1822 that Austrian mineralogist F. Mohs proposed a relative, broadly quantitative “scale of hardness” of minerals assigning values between 1 and 10. Since then, the Mohs’ Scale of Hardness for Minerals has been universally adopted. All minerals, when pure, have been found to have a fairly constant hardness value on this scale and hence the importance of hardness as a diagnostic property.
The Mohs’ scale of hardness comprises ten minerals arranged in order of ascending hardness; the softest is assigned a value of 1 and the hardest a value of 10. (Table 9.1)
In practice, hardness of any mineral can be determined with the help of minerals from the above scale. The harder mineral will scratch the softer mineral. By starting with mineral of lowest hardness from the scale, hardness of unknown mineral can be easily fixed.
For instance, an unknown mineral is not scratched by fluorite (H = 4) but is scratched by apatite (H = 5). Hence its hardness lies between 5 and 4, and may be fixed at 4.5. It must also be remembered that minerals of equal hardness scratch each other (diamond cuts diamond).
Some common materials have been assigned hardness values according to Mohs scale and may prove useful in determination of hardness of an unknown mineral quickly. These are Brass (H = 3), Glass (H = 5.5), Steel (H = 6). Hardness of a human finger nail varies between 1.5 to 2.5.
Three facts need careful consideration in determining hardness of a mineral on Mohs scale:
First:
Hardness is only a relative property. If Talc has H = 1 and Quartz H = 7, it does not indicate quartz is seven times harder than talc.
Second:
Hardness is an anisotropic property; a mineral may show different values in different directions. Most commonly, however, this difference is negligible except in the case of a mineral kyanite where H = 4.5 along the length and H = 6.5 across the length of a crystal.
Third:
Hardness decreases on decomposition of a mineral due to atmospheric attack on its surface. Hence, it must be checked on unweathered and unaltered surfaces only.
5. Cleavage:
It is defined as the tendency of a crystallized mineral to break along certain definite directions yielding more or less smooth, plane surfaces. In other words, cleavage planes are the planes of easiest fractures, and are essentially indicative of directions of least cohesion in the atomic constitution of a mineral.
A mineral may have cleavage in one, two or three directions. Further, the degree of ease in splitting along cleavage directions may vary in the same mineral. As such cleavage is described both in terms of number of directions in which it is observed on a mineral and also in terms of degree of perfect splitting.
Since cleavage directions are always parallel to certain crystal faces in a mineral, these may be described as such. For instance, cubic cleavage (galena and haylite), rhombohedral cleavage (calcite) and prismatic cleavage, basal cleavage and octahedral cleavage.
In terms of perfection, the cleavage is described as: eminent, perfect, good, distinct and indistinct in that order. In eminent cleavage, the mineral can be spilt very easily yielding extremely smooth surfaces e.g. in mica. Perfect cleavages are seen in orthoclase and calcite.
Parting:
It is a property of minerals by virtue of which it can split easily along certain secondary planes. Although it may be confused at first with cleavage but its true nature can be established by careful study.
Parting is actually due to the presence of secondary twin-planes and gliding planes along which the mineral may split easily. These (parting surfaces) are not necessarily related to the mineral as a species, that is, they may be present in one specimen and absent in the other specimen of the same mineral.
Parting is attributed to the presence of a substance of different composition along the parting planes or to the stresses that might have operated during or after the formation of the particular crystals. Best example of parting can be seen in corundum where cleavage may be absent but parting may be very prominent.
6. Fracture:
The appearance of the broken surface of a mineral in a direction other than that of cleavage is generally expressed by the term fracture. In some cases fracture becomes a characteristic property of a mineral.
Common types of fractures are:
(i) Even:
When the broken surface is smooth and flat. Example- chert.
(ii) Uneven:
When the mineral breaks with an irregular surface which is full of minute ridges and depressions. It is a common fracture of many minerals. Example- Fluorite.
(iii) Conchoidal:
The broken surface of the mineral shows broadly concentric rings or concavities which may be deep or faint in outline. In the latter case, the fracture may be termed as subconchoidal. Example: Quartz.
(iv) Splintery:
When the mineral breaks with a rough woody fracture resulting in rough projection at the surface. Example- kyanite.
(v) Hackly:
The broken surface is highly irregular with numerous sharp, fine, pinching projections. Example- Native Copper.
(vi) Earthy:
The surface is smooth, soft and porous. Example- Chalk.
7. Tenacity:
The behaviour of a mineral towards the forces that tend to break, bend, cut or crush it is described by the term tenacity. Thus, when a mineral can be cut with a knife, it is described as sectile. If the slices cut out of it can be flattened under a hammer, it is said to be malleable. Most minerals exhibit the property of brittleness, by virtue of which they change into fine grains or powder when scratched with a knife or when brought under the hammer.
A mineral is said to be flexible when it can be bent, especially in thin sheets. Chlorites are flexible. Some minerals are not only flexible but elastic, that is, they regain their shape when the force applied on them is removed. Micas are best example. The flexible and elastic fibres of asbestos can be woven into fire-proof fabric.
As such, in terms of tenacity mineral may be sectile, brittle, flexible, plastic and elastic, the last two qualities being of diagnostic importance.
8. Structure (Form):
Minerals often occur in characteristic body forms or physical shapes. The physical make up of a mineral is expressed by the term structure and is often helpful in identifying a particular mineral. In reality, structure merely shows the habit in which the crystal or crystalline substance making a mineral tends to occur in nature. Following are a few common structural forms (habits) observed in minerals.
(i) Tabular:
The mineral occurs in the form of a flattened, square, rectangular or rhombohedral shape. In other words, flattening is conspicuous compared to lengthwise elongation. Examples- Calcite, orthoclase, barite etc.
(ii) Elongated:
When the mineral is in the form of a thin or thick elongated, column-like crystals. Examples- Beryl, quartz, hornblende. It is also commonly referred as a columnar structure.
(iii) Bladed:
The mineral appears as if composed of thin, flat, blade-like overlapping or juxtaposed parts. Example- Kyanite
(iv) Lamellar:
The mineral is made up of relatively thick, flexible, leaf-like sheets. Example- Vermiculite.
(v) Foliated:
The structure is similar to lamellar in broader sense but in this case the individual sheets are paper thin, even thinner and can be easily separated. Example- Muscovite (mica).
(vi) Fibrous:
When the mineral is composed of fibres, generally separable, either quite easily (example- asbestos) or with some difficulty (example- gypsum).
(vii) Radiating:
The mineral is made up of needle like or fibrous crystals which appear originating from a common point thereby giving a radiating appearance. Example- Iron pyrites. When needles are pointed and not necessarily radiating, the structure is called acicular.
(viii) Granular:
The mineral occurs in the form of densely packed mass of small grain-like crystals. Example- Chromite.
(ix) Globular:
Globular or botroiydal, when the mineral surface is in the form of rounded, bulb-like overlapping globules or projections. Example- Hematite.
(x) Reniform:
It is similar to globular but the shape of the bulbs or projections resembles to human kidneys. Example- Hematite.
(xi) Mammillary:
It is similar to globular but the projections are conspicuous in size, overlapping in arrangement and rounded in shape. Example- Malachite.
9. Specific Gravity:
The density of a substance is a fundamental property of great significance and is defined as the mass per unit volume of the substance. For minerals, it is expressed in g/cc.
In mineralogy, the term specific gravity is used more frequently than density and signifies “the ratio between the density of a mineral and that of water at 4° Celsius”. Since it is a ratio, it has no units. Specific gravity of quartz is, for instance, 2.65. The specific gravity is also termed relative density.
Density (hence specific gravity) of minerals depends primarily on:
(i) Composition:
The non-metallic minerals have low values, ranging between 2.5 to 4.5 g/cc, whereas metallic minerals and ores have densities as high as 20 g/cc.
(ii) Atomic Constitution:
Minerals with atoms of greater atomic radii show less density values compared with those made of atoms of smaller atomic radii.
Since temperature and pressure are both known to change volume of a substance, it follows that density will also show a change when a mineral is subjected to elevated temperature or high pressures.
Specific gravity of some common minerals is: quartz (2.65); calaite (2.60); fluorite (3.18); hematite (5.2); chalcopyrite (4.2); galena (7.5); native gold (19.3).
Determination:
Many methods and instruments are available for determination of specific gravity of minerals. All of them involve weighing the mineral specimen in air and then in a liquid (generally water), wherefrom the loss in weight of the mineral is obtained which is due to the displacement of an equal volume of the liquid.
Specific gravity is calculated by the following relationship:
Sp.Gr. = (Weight of the mineral in air/Loss of weight in liquid) × d
where d = density of the liquid used. (In the case of water it is 1)
The Jolly’s balance, the Beam balance and the Walker’s Steelyard Balance are commonly used in the geological laboratories for determination of specific gravity of minerals.
These are all very simple yet delicate instruments and require:
(a) Careful selection of the sample from the mineral; the grain should be small in weight, free from dust and other impurities;
(b) Careful handling, as a slight error in adjustment and observation can give rise to incorrect values.
When used carefully, value of specific gravity correct to the second point of decimal can be found with these methods:
1. The Jolly’s Balance:
It consists of an upright stand provided with a mirror and graduated scale and a sliding rod, which can be lowered or raised. A movable stand for keeping a beaker on it is attached to the main stand. (Fig. 9.11). A spring in standard tension and having a bead is hung from the top screw of the sliding rod. The spring has to its lower end two small pans hooked one below the other.
For finding specific gravity of a mineral grain, the spring is properly adjusted. The position of the spring bead is first noted on the graduated scale while the lower pan is immersed in water and upper pan is kept out of it. Let this reading be ‘a’. The mineral grain is then put in the upper pan; the spring moves down and the new position of the bead as reflection in the graduated scale is read carefully. Let it be ‘b’. The reading b-a gives the weight of the substance in air.
The grain is now transferred to the lower pan which remains immersed in water. The spring will move up slightly and new position of the bead is noted. Let it be ‘c’. Then b-c gives the loss in weight of the mineral in water.
Specific gravity is then calculated using following relationship:
2. The Beam Balance:
It consists of following parts:
(a) A graduated beam balanced on two supports held on a base.
(b) Two pans, an upper and a lower, attached to the shorter end of the beam.
(c) Three riders R, r1, and r2, of which R is principal rider placed on the shorter end and the other two on the longer end. (Fig. 9.12)
Working:
Balance the beam first by adjusting the principal rider R on the shorter arm and rider r1 on the longer arm. These riders should not be moved any further during subsequent steps.
Place the mineral in upper pan while lower pan is kept immersed in water. The equilibrium will be disturbed; balance the beam again with the help of the third rider r2 moving it on the longer arm. Read this position of rider r2; let it be ‘a’.
Now transfer the mineral from the upper pan to the lower pan which is kept freely suspended in water. Balance the beam once again by moving rider r2. Let this position be ‘b’. Then,
3. Walker’s Steelyard Balance:
This instrument is broadly similar in appearance to the beam balance but differs in principle. It consists of a graduated beam, the shorter arm of which is provided with a rider, R. The beam is pivoted on a vertical support.
Working:
Balance the beam by adjusting the rider R on the shorter arm. Suspend the mineral specimen tied with a fine thread on the graduated arm. Move the specimen along the beam till the beam is again balanced. Let this position be ‘a’. Now keep a beaker three fourths full of water below the suspended specimen so that the latter is completely immersed.
Move the specimen (and the beaker) till the beam is again balanced. Let this new reading be ‘b’. As the balance works on the principle of levers, these readings are inversely proportional to the weights of the mineral in air and in water respectively. Therefore,
The Pycnometer Method:
It is used for determining specific gravity of fine sediments or mineral samples in powdered form. Pycnometer is a small glass bottle with a stopper. In this method, the bottle is first weighted empty (w1), and then with a small quantity of the mineral powder (w2). It is then filled with a given liquid (water can be used), and weighted again. Let this weight be (w3).
It is emptied, cleaned thoroughly and filled with the same liquid once again. It is weighed. Let this weight be (w4).
From the above weights, specific gravity is calculated by using the following relationship:
where d is gravity of the liquid used. For water it is taken as 1.
X-rays have also been used to determine the density of minerals. In these methods it is the spacing of constituent atoms per unit volume or ‘packing index’, which is determined first and from that density of the substance is calculated.
10. Form:
It is the internal atomic arrangement of a mineral which is manifested outwardly by development of geometrical shapes or crystal characters. One of the following three terms may describe the form of a mineral.
(i) Crystallized:
When the mineral occurs in the form of well-defined crystals as represented by crystal faces and angles or when it shows perfect cleavage, which is also indicative of perfect atomic arrangement.
(ii) Crystalline:
When well-defined crystals are absent but the mineral shows a clear tendency towards crystallisation as evidenced by development of small grains each of which is virtually an incipient crystal.
(iii) Amorphous:
Neither a crystal face nor a cleavage is seen. There is no evidence of orderly arrangement of atoms.
Miscellaneous:
Besides the above properties, minerals may show some specific and rare qualities that often become helpful in their identification.
Some of these special properties are explained below:
(i) Magnetism:
Some minerals have natural magnetism in them to an appreciable extent. Example- magnetite. A few other minerals may be only feebly magnetic. Example- spinels, tourmaline.
(ii) Electricity:
In some minerals an electric charge may be developed by heating. These are called pyroelectric minerals. Examples- tourmaline, boracite, quartz. In some other minerals, the same effect of developing a charge may be produced by applying pressure. This group is termed as piezo-electric. Examples- tourmaline and quartz.
(iii) Fluorescence:
A few minerals have the property of glowing or emitting light when they are exposed to radiation. This property is called fluorescence and mineral fluorite shows it.
(iv) Phosphorescence:
It is similar to fluorescence in essential character but in this case light is emitted by mineral not during the act of exposure to radiation but after the substance is transferred rapidly to a dark place. Fluorite, quartz, willemite and diamond show phosphorescence under different conditions.
(v) Fusibility:
Minerals behave differently on heating to elevated temperature. Some fuse (melt) easily at lower temperatures whereas others require very high temperatures.
A scale of fusibility has been suggested by Von Kobell. It consists of six minerals arranged according to temperature of fusion- stibnite (525° C), Natrolite (965° C), Almandine (1,200° C), Actinolite (1,296° C), Orthoclase (1,300° C), and Bronzite (1,380° C).
Optical Properties of Minerals:
Such properties of a mineral which are related to the behaviour of light while being transmitted through or reflected from it are grouped under optical properties. They are of great significance in the determinative mineralogy and highly useful in identifying individual minerals occurring in very small, physically inconspicuous grain size, as for examples in rocks.
Study of optical properties of a mineral requires that:
(i) The mineral must be first cut into as thin as possible a section so that light is easily transmitted through it, or, if the mineral is of an opaque nature, light can be uniformly reflected from its surface. Such a section is called a thin section of a mineral or rock. These sections are prepared carefully and mounted on glass slides.
(ii) The student should have a working knowledge of basic properties of light and should also be conversant with properties of glasses, mirrors, lenses and prisms.
Following is only a very brief review of common phenomena connected with light which are used for investigating the optical properties of minerals.
1. Light:
It is defined as an electromagnetic phenomenon involving essentially of waves — the light waves — which are caused by certain periodic changes in the energy given off by vibrating electrons.
2. Ordinary Light:
In such light the vibrations take place in all possible directions but within a plane essentially at right angles to the direction of propagation. The ordinary light, also referred as white light, has a visible spectrum of seven colours with violet being at one end and red being at the other end.
3. Polarised Light:
When it is possible to obtain a condition in which the light vibrates only in one direction in the plane of vibration, the light is said as polarized (sometime plane – polarized) and the condition or process as polarization.
Polarised light can be obtained by one of three methods:
(i) By reflection,
(ii) By absorption,
(iii) By refraction.
For obtaining polarised light by reflection a smooth surface is used to reflect the light. This method, however, gives only partial polarisation.
In the absorption method, materials haying a capacity of selective absorption for light are used to obtain polarised light. A plate cut from synthetic material Polaroid or from natural mineral tourmaline will allow only that light to pass through it which vibrates along a particular direction.
In the refraction method for obtaining polarised light, use is made of special prisms named after their inventors as Nicol prism and Ahren prism. The Nicol prism is actually a cleavage piece of mineral calcite (also called Iceland spar) that has been specially ground at edges, cut diagonally into two, polished and cemented together in such a way that an incident ray falling on it gets doubly refracted (explained below).
Only one of the resulting two refracted rays (the extra-ordinary ray) is allowed to pass through the prism. The Ahrens prisms are also similar to Nicol prism in principle but are simpler in construction. These are rectangular in shape.
The prisms made for polarizing the light on the basis of refraction are very commonly used in the optical instruments. They are commonly referred as nicols whether they are of first or second design.
4. Refractive Index:
It is known that when a ray of light passes from one medium to another of a different density, it gets refracted from its normal course. The ratio between the sine of angles of incidence and refraction is expressed by the term refractive index.
It is given by the relation:
n = sin i/sin r
where n = refractive index, i = angle of incidence, r = angle of refraction
When the two media are air and the mineral, the values obtained indicate the refractive index of the mineral with respect to air. Thus, n for glass = 1.608, for garnet = 1.75, and for diamond = 2.42.
It may be mentioned here that according to the law of refraction the velocity of light in a substance is proportional to the reciprocal of its refractive index. Minerals with higher refractive indices will allow the light to pass through them at lower velocities compared with minerals of lower refractive indices.
The refractive index of a mineral is an important property studied in thin sections under a microscope. It helps in identifying a mineral from other minerals, especially when they are lying in close contact as in a rock. Many different laboratory techniques are available for this purpose.
5. Dispersion:
This is a phenomenon depending on the refractive index of a substance. Ordinary light is made up of a spectrum of seven types of radiation – violet being at one end and red at the other end of spectrum. When a medium is capable of breaking the light into its component colours during transmission, as a prism of glass, each component is refracted at a characteristic rate which is different from that of the adjoining radiation.
The net result is difference in velocities of the component colour radiations within the body of the medium. This difference in the index of refraction for the various radiations results in a brilliance. This is characteristic property of gems. Higher the refractive index, greater is the dispersion of light. For example, in diamond, the red end of spectrum has a refractive index of 2.407 and the violet end 2.465, difference (0.058) being of a very high order.
6. Total Reflection:
It is the property of light that when it passes from a denser medium to a rarer medium (e.g. from water to air) it gets refracted away from the normal. In all such cases, a stage is reached when at a particular angle of incidence; the angle of refraction is 90°. This angle of incidence is called critical angle.
All the incident rays impinging upon the medium beyond this angle will be reflected backwards into the medium rather than getting refracted. The phenomenon of reflection of an incident ray back into the same medium is called total internal reflection. It has been established that substances of higher refractive index have lower critical angles and vice-versa. The critical angle of diamond, for instance, is 24°26′ with respect to air.
7. Double Refraction:
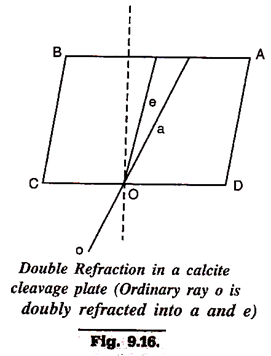
It is one of very significant properties of some solids, especially minerals and has proved highly useful in their identification. When a ray of light passes through such minerals, it is not only refracted but also resolved into two rays, each having its own velocity and hence separate index of refraction. All minerals (and artificially crystallised substances) except those crytallising in cubic system show this property of double refraction (Fig. 9.16).
The two rays resulting from a single incident ray are designated as ordinary ray (symbol a) and extra-ordinary ray (symbol e). It is characteristic of a that it has same velocity in all directions in a given substance while the extra-ordinary ray, e, has different velocity in different directions in the same substance. Again, in some minerals, the velocity of a, though constant, may be higher than that of e, whereas in other minerals it may be e, which has a higher velocity. This factor gives another basis for optical classification of minerals.
8. Birefringence:
This is a phenomenon related to the property of double refraction. Each of the two rays (ordinary, a, and extra-ordinary, e) will have its own refractive index with respect to the same medium. The difference in the refractive indices of these rays is expressed by the term birefringence and indicates the degree of double refraction in a substance.
9. Isotropic Substances:
Those substances which do not show the phenomenon of double refraction are called isotropic. In these, the refractive index of light is uniform in all directions. Minerals belonging to isometric system are all isotropic in character. Some examples are- diamond, garnet, halite and galena.
10. Anisotropic Substances:
When a substance, such as a mineral shows double refraction, that is, in which an incident ray of light is broken into two rays, which travel with different velocities thereby causing a variation in the property of refractive index in different directions, it is called anisotropic. Minerals belonging to all crystallographic systems except cubic system are anisotropic in character.
Quartz, calcite, fluorite, gypsum, tourmaline and topaz are just a few examples out of hundreds of such minerals.
11. Optic Axis:
It is a direction in an anisotropic substance in which there is no double refraction. This term is relevant only in anisotropic substances because in isotropic substances double refraction does not occur at all.
In anisotropic substances, there may be one or two such directions in which the phenomenon of double refraction is not observed. These directions are expressed by the term optic axes.
Minerals are further distinguished as optically uni-axial if there is only one-optic axis and as optically biaxial if there are two optic axes or directions of “no double refraction”.
The mineral crystallising in Tetragonal and Hexagonal systems are optically uniaxial, whereas minerals crystallising in Orthorhombic, Monoclinic and Triclinic systems are optically biaxial.
12. Optical Sign:
While studying optical properties of a mineral in thin sections under a microscope, it is also usual to determine its optical sign, that is, whether it is optically positive (+) or optically negative (-). This is done on the basis of the relative velocity of the two rays into which the incident ray is resolved on double refraction.
In uniaxial minerals, a mineral is said to be:
(i) Optically positive (+), if the velocity of ordinary ray, (a), is greater than that of extraordinary ray (e). (It is same thing as saying the refractive index of extra-ordinary ray is higher than that of ordinary ray because refractive index is reciprocal of velocity of the ray.)
(ii) Optically negative (-), if the velocity of the extra ordinary ray is greater than that of the ordinary ray.
In the biaxial minerals, there are three vibration directions distinguished as X (fastest), Y (intermediate) and Z (slowest), with corresponding refractive indices as α, β and γ respectively.
In order to determine the optical sign of such a mineral, following considerations are kept in mind:
(i) As there are two optic axes,
(ii) As these may be inclined to each other at an angle, called the optic axial angle, which may be acute or obtuse,
(iii) As X or Z vibration direction may be the bisectrix of the optic axial angle.
A biaxial mineral is described as optically positive (+), if Z is the acute bisectrix and optically negative (-), if X is the acute bisectrix.