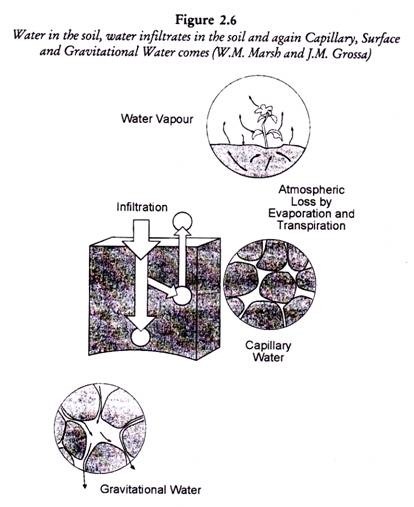
ADVERTISEMENTS:
It has been observed that all the crystals of minerals and synthetic substances studied so far can be grouped, on the basis of A – Closed form, B – Open form symmetry, into 32 (Thirty two) classes. These are often called crystal classes. By definition, all crystals with an external form of the same symmetry make a crystal class.
All the crystals (and hence crystal classes) when referred to the crystallographic axes, can be conveniently grouped into six major crystal systems.
These systems, in order of decreasing symmetry are:
ADVERTISEMENTS:
1. Isometric (Cubic) System;
2. Tetragonal System;
3. Hexagonal System;
4. Orthorhombic System;
5. Monoclinic System; and
ADVERTISEMENTS:
6. Triclinic System.
Of these, the Hexagonal System is further divided into two divisions- The Hexagonal Division and the Rhombohedral Division.
In common practice, study of crystallography involves referring any given crystal to the three (or four, in one case) crystallographic axes; thereby its crystal system is found. Then, its symmetry elements are determined in desired detail to place it in a proper symmetry class. Finally, various forms developed on it are carefully studied determining parameters, indices and symbols in each case.
ADVERTISEMENTS:
An attempt has been made to describe the salient features of the six crystallographic systems as briefly as possible and also in accordance with the set pattern.
1. Isometric (Cubic) System:
Definition:
All those crystals that can be referred to three crystallographic axes, which are- (i) essentially equal in length, (ii) at right angles to each other, and (iii) mutually interchangeable, are said to belong to the isomeric or cubic system.
Axial Diagram:
Since all the three axes are equal and interchangeable, these are represented by the letter a. In the study position, however, the axes may be designated as a1, a2 and a3 the last being vertical. (Fig. 10.16.)
Classes:
Five Symmetry classes fall in the Isometric System by virtue of their symmetry. The normal class is known as galena type.
It has got the following symmetry:
ADVERTISEMENTS:
(a) Axes of Symmetry:
13 in all.
3 are axes of four-fold symmetry;
4 are axes of three-fold symmetry;
6 are axes of two-fold symmetry.
The three axes of four-fold symmetry are chosen as the crystallographic axes.
(b) Planes of Symmetry:
9 in all.
3 planes of symmetry are at right angles to each other and are termed the principal (axial) planes;
6 planes of symmetry are diagonal in position and bisect the angles between the principal planes.
(c) It has a Centre of symmetry.
Forms:
Following are the forms that commonly develop in the crystals belonging to Isometric System:
i. Cube:
A form bounded by six similar square faces, each of which is parallel to two of three crystallographic axes and meets the third axis. Symbol (100). Fig. 10.17A.
ii. Octahedron:
A form bounded by eight similar faces, each of the shape of an equilateral triangle, each meeting the three crystallographic axes at equal distances. Symbol- (111), Fig. 10.17B.
iii. Dodecahedron:
It is a form with twelve similar faces each of which is parallel to one of the three crystallographic axes and meets the other two at equal distances. (Fig. 10.17 C), Symbol (101)
iv. Trisoctahedron (hhl):
A form of twenty four (24) faces; each face meeting two axes at unit length and to the third at greater than unity. Faces occur in eight groups of three each.
v. Trapezohedron (hll):
A form of twenty four (24) faces each face meeting one axes at unit length and to the other two at greater than unity. Each face is a trapezium.
vi. Tetra-Hexahedron (hol):
Twenty four (24) faces; each face is parallel to one axis and meets other two at unequal distance which are simple multiple of each other; faces occur in six groups of four each.
vii. Hexaocatahedron (hkl):
Forty eight (48) faces; each face meets the three axis at unequal distances.
Other Classes:
Isometric system comprises five symmetry classes in all.
Beside the normal class, following three classes are also represented among the minerals:
A. Pyritohedral Class (Pyrite Type):
(a) Symmetry:
7 Axes of symmetry, of which, 3 are axial axes of two-fold symmetry, 4 are diagonal axes of two fold symmetry. 3 Planes of symmetry. A Centre of symmetry.
(b) Forms:
Pyritohedron and Diploid are two typical forms of this symmetry class. Pyritohedron is a hemihedral form having twelve faces and a general symbol (hko) Fig. 10.18 A.
Diploid is a closed form of twenty-four faces that typically occur in pairs (hence the name) and have a symbol (hki) Fig.10.18B.
B. Tetrahedral Class (Tetrahedrite Type):
(a) Symmetry:
7 axes of symmetry (as in pyrite type), 6 planes of symmetry, diagonal, no center of symmetry.
(b) Forms:
Most typical form of this class is a four sided solid in which each face is an equilateral triangle. It is termed tetrahedron. It has a general symbol of (111). Fig. 10.18C.
C. Plagiohedral Class (Cuprite Type):
(a) Symmetry:
13 axes of symmetry (as in normal class) No planes of symmetry. No Centre of symmetry.
(b) Forms:
Icositedraherons, each of 24 faces, with a symbol (hkl) and commonly enantiomorphous in character are typical forms of this class.
Examples of Isometric Minerals:
A vast number of common minerals crystallize in isometric system.
Following are few examples:
i. Galena
ii. Pyrite
iii. Sphalerite
iv. Spinel
v. Magnetite
vi. Sodalite
vii. Garnet
viii. Diamond
ix. Flourite
x. Leucite.
2. Tetragonal System:
Definition:
The tetragonal system includes all those crystals which can be referred to three crystallographic axes so that:
(i) Two axes are equal, interchangeable and horizontal in position;
(ii) The third axis is either longer or shorter than the other two and is vertical in position; and
(iii) All the three axes are mutually at right angles to each other.
Axial Diagram:
In study position, the crystal is so held that the longer or shorter axis is vertical in position. The one of the horizontal axes is made to run parallel to the observer and the other form front backward. (Fig. 10.20.)
The horizontal axis running away from the observer is designated as a1, that running from right to left is a2, and the vertical axis is designated as c axis.
Axial ratio for the crystal of this system is expressed as a: c.
Classes:
The Tetragonal system includes seven symmetry classes.
Normal Class (Zircon Type):
The symmetry of the normal class (Zircon type) is as follows:
(a) Axis of Symmetry:
5 in all; of these, 2 axes are horizontal and of two fold symmetry, 2 axes are horizontal bisecting the angles made by first set of horizontal axis; they are also of two fold symmetry. 1 axis is vertical and of four folds symmetry (hence tetragonal forms).
(b) Planes of symmetry:
5 in all; of these, 1 plane is horizontal, 2 planes are vertical, 2 planes are vertical diagonal. There is a centre of symmetry.
Forms:
Following forms are met with in the crystals of the Tetragonal System:
a. Basal Pinacoid (001):
An open form with two similar faces. Each face is parallel to the two horizontal crystallographic axes and meets the third, vertical axis at unit length. (Fig. 10.21 A)
b. Prisms:
These are open forms of four or eight faces in which each face is essentially parallel to the vertical crystallographic axes.
Depending on their relation with the other two axes, three types of prisms are recognized in the tetragonal system:
(i) Prism of First Order (110):
Four faces each face meeting the two horizontal axes – at unit lengths and being parallel to the vertical axis (Fig. 10.21B);
(ii) Prism of Second Order (100):
Four faces; each face intercepts only one of the horizontal axes and is parallel to the second axis besides being parallel to the vertical axis (Fig. 10.21 B-100).
(iii) Prism of Third Order or Ditetragonal Prism (hko):
Eight faces each face intercepting the two horizontal axes at different lengths; e.g. 210, 310.
c. Pyramids:
These are closed forms of eight or sixteen faces in which each face essentially meets the vertical crystallographic axis.
Three types of pyramids are recognized on the basis of their relationship with other crystallographic axis:
(i) Pyramid of First Order (hhl):
Eight faces; each face cuts the two horizontal axis at equal length besides intersecting the vertical axis. Example- (221), (223), (111) (Fig. 10.21C)
(ii) Pyramid of Second Order (hol):
Eight faces; each face cuts only one of the two horizontal axes; it is parallel with one horizontal crystallographic axis, Example- (201), (101). (Fig. 10.21D)
(iii) Pyramid of Third Order (hkl):
Also called ditetragonal pyramid is a closed form of 16 faces in which each face cuts all the three crystallographic axes at unequal lengths. Example- (321), (421).
Other Classes:
Of the remaining six classes, the following three are well represented among minerals:
a. Tripyramidal class;
b. Pyramidal Hemimorphic class;
c. Sphenoidal class.
Examples of Tetragonal Minerals:
i. Zircon
ii. Vesuvianite
iii. Rutile
iv. Wernerite
v. Cassiterite
vi. Octahedrite
vii. Chalcopyrite
viii. Scheelite
ix. Wulfenite
x. Braunite.
3. Hexagonal System:
Definition:
All those crystals which can be referred to four crystallographic axes of which:
(i) Three axes are horizontal, equal, interchangeable and intersecting each other at 120° between the positive ends.
(ii) The fourth axis is vertical and at right angles to the three horizontal axes, is grouped under Hexagonal System.
Axial Diagram:
The horizontal axes, all being equal, are designated by the letter a (a1, a2, a3), and the vertical axis by the letter ‘c’ as usual. (Fig. 10.23)
Divisions:
The Hexagonal System consists of two distinct divisions, namely the hexagonal division and the rhombohedral (trigonal) division. The first includes 7 crystal classes and the second 5 crystal classes.
The two divisions will be described individually:
A. The Hexagonal Division:
Symmetry of Normal Class
(a) Axis of Symmetry:
7 in all. 1 axis, vertical, of six fold symmetry; 6 axes, horizontal, of two fold symmetry;
(b) Planes of Symmetry:
7 in all, 1 plane, horizontal, containing 6 axes of symmetry. 6 planes, vertical and vertical diagonal. And a Centre of Symmetry.
Forms:
Forms of hexagonal system differ in character from forms of all the other systems in that their parameters, indices and symbols are determined with respect to four crystallographic axes (and not three as in other systems). Thus, the relation of any hexagonal form is expressed by the general term, (hkil).
It may further be pointed out here that h + k + i = 0 is a typical relation true for all the forms belonging to the hexagonal system.
1. Base (0001):
An open form of two faces in which each face meets the vertical axis only. (Fig. 10.24.)
2. Prisms:
A prism is an open form in which each face is essentially parallel to the vertical axis.
Following three types of prisms are met with in the Hexagonal system:
(a) Prism of First Order (101̅0):
An open form of six faces in which each face is parallel to one of the three horizontal axes besides the vertical axis. It cuts the two horizontal axes at unit length. (Fig. 10.24)
(b) Prism of Second Order (112̅0):
An open form of six faces like prism of 1st Order but in this case each face cuts all the three horizontal axes, two axes at equal length and to the third at greater length. It is, of course, parallel to the vertical axis.
(c) Prism of Third Order (hki̅o):
It is also called a dihexagonal prism as it has double the number of faces (twelve), compared to the six faces of prism of 1st order. In this form each face cuts all three horizontal axes at unequal lengths.
Pyramids:
A pyramid is a form that essentially intercepts the vertical axis.
Like prisms, three types of pyramids occur in hexagonal system:
(i) Pyramid of First order (101̅1):
It is a closed form of twelve faces, six above and six below the horizontal plane, each face essentially cutting the vertical axis and two of the three horizontal axes. It is parallel to the third horizontal axis. (Fig. 10.24)
(ii) Pyramid of Second Order (hh2h̅l):
It is also a closed form of twelve faces but in this each face cuts all the three horizontal axes, two of them at unit length and the third at double the length. It also cuts the vertical axis.
(iii) Pyramid of Third Order (hki̅l):
It is also called dihexagonal pyramid, as it has double the number of faces (24) of an ordinary hexagonal pyramid. Each face in dihexagonal pyramid cuts all the four crystallographic axes at unequal lengths.
B. Rhombohedral Division:
Symmetry:
The Normal Class of Rhombohedral Division has the following symmetry:
(i) Axis of Symmetry:
4 in all. 1 vertical axis of three fold symmetry. 3 horizontal axes of two fold symmetry.
(ii) Planes of Symmetry:
3 in all. All the planes are vertical diagonal in position. A center of Symmetry.
Forms:
a. Rhombohedron:
The most common form of this group is a rhombohedron, a solid bounded by six similar faces, each like a rhomb and meeting the vertical axis. Of the three horizontal crystallographic axes, each face of rhombohedron meets the two axes and is parallel to the third. (Fig. 10.25). The rhombohedron has a symbol of (101̅1).
The usual method to hold rhombohedron in a study position is along its vertical axis (c-axis) which joins the two trihedral angles, also called the pole angles. (Fig. 10.25). In such a position, the three horizontal axes join the middle points of the other sides.
The rhombohedron is further distinguished into an obtuse type or an acute type, depending upon the value of the pole angle which in turn depends on the axial ratio a: c.
As a general rule, greater the length of the ‘c’ axis with respect to the a-axis, more acute is the rhombohedron.
Rhombohedrons are also distinguished into positive and negative types. When in a study position (as described above) the rhombohedron presents a full face to the observer, it is taken to be a positive type; when, however, an edge is in front of the observer in the study position, it is designated as a negative rhombohedron.
The two types together make a complete double six-sided hexagonal bipyramid.
b. Scalenohedrons:
These are the next common forms of Rhombohedral division. A scalenohedron is a closed form of 12 faces, each face being a scalene triangle. Its symbol is (hkil). Like Rhombohedron, these forms may also be positive and negative in character. Each scalenohedron has 12 polar angles, of which six are acute angles and six are obtuse angles. The ratio of a: c determines if a scalenohedron is obtuse or acute.
Examples of Minerals:
i. Quartz
ii. Corundum
iii. Tourmaline
iv. Calcite
v. Beryl
vi. Hematite
vii. Brucite
viii. Cancrinite
ix. Willemite
x. Chabazite
4. Orthorhombic System:
Definition:
This system includes all those crystals which can be referred to three crystallographic axes, all of which are:
(i) Essentially unequal in length
(ii) Essentially at right angles to each other.
Axial Diagram:
The three crystallographic axes are arbitrarily designated as a, b and c, in such a way that the c axes is vertical and the b axis runs from right to left and the a axis extends from front to back in the crystal when held in a proper study position.
The b axis is always longer of the two horizontal axes and is also designated as macro axis.
The a axis being shorter, is designated as brachy axis. (Fig. 10.29.)
In the determination of the Axial Ratio in the crystals of the Orthorhombic System, it is customary to take the length of ‘b’ axis as unity and express the lengths of the other axes in terms of this unit.
Symmetry of Normal Class:
The system includes three classes. The symmetry of Normal Class (Baryte Type) is given below:
(a) Axis of Symmetry:
3 in all, of two fold symmetry.
(b) Planes of Symmetry:
3 in all, axial in position. A Centre of Symmetry.
Forms:
Common forms developed in the normal class of the Orthorhombic Systems are:
A. Pinacoids:
A Pinacoid is an open form of two faces in which each face meets any one of the three axes and is parallel to the other two axes. A typical symbol is (100). Three types of pinacoids are known in the Orthorhombic System.
(i) a-Pinacoid or Macropinacoid (100):
An open form of two faces, each face cutting the a- axis and being parallel to the other two faces.
(ii) b-Pinacoid or Brachy pinacoid (010):
An open form of two faces, each face cutting the b-axis and being parallel to the other two axes.
(iii) c-Pinacoid or Base (001):
An open form of two faces, each face cutting the c-axis and being parallel to the two horizontal axes.
B. Prisms:
A prism is a form which is essentially parallel to the vertical axis.
Three types of prisms are recognized in the Orthorhombic System:
(i) Unit Prism (110):
An open form of four faces in which each face makes intercepts on the horizontal axes corresponding to the assumed axial ratio for the species. (Fig. 10.30).
(ii) Macroprism (hko, h>k):
An open form of four faces in such a way that each face cuts the brachy axis at a greater length. It is parallel to the vertical axes. Example (210). Faces lie between those of macropinacoids and unit prism.
(iii) Brachyprism (hko; h<k):
An open form of four faces in such a way that each face cuts the brachy axis at a smaller length than the macroaxis. Faces of this form lie between the brachypinacoid and the unit prism.
C. Domes:
A dome is defined as forms whose faces essentially meet the vertical axis and are parallel to one of the two horizontal axes.
Two types of domes are distinguished:
(i) Macrodome (hol):
An open form of two faces in which each face meets the vertical axis and the a-axis, and is parallel to the macroaxis.
(ii) Brachydome (Ohl):
An open form of two faces, each face is parallel to the brachy axis and meets the other two axes. (Fig. 10.30 A and B)
D. Pyramids:
In these forms of four faces, each face essentially meets the vertical axis.
Three types of pyramids are recognized:
(i) Unit Pyramid (hhl):
Where the parameters correspond to the assumed axial ratio for the species.
(ii) Macro Pyramid (hkl, h>k):
A closed form of four faces, each face intercepting all the three axes at unequal lengths in such a way that intercepts at a-axis is greater than those at b-axis; e.g. (214).
(iii) Brachy Pyramid (hkl; h<k):
A closed form of four faces in which intercepts at b-axis are greater than those made at a-axis, e.g. (241). (Fig. 10.30)
Examples of Orthorhombic Minerals:
i. Sulphur
ii. Staurolite
iii. Andalusite
iv. Topaz
v. Barytes
vi. Aragonite
vii. Enstatite
viii. Anthophyllite
ix. Stibnite
x. Calamine.
5. Monoclinic System:
Definition:
The Monoclinic System includes all those forms that can be referred to three crystallographic axes which are essentially unequal in length and further that one of these is always inclined. (Mono = single, clino = inclined).
Axial Diagram:
Since all the three axes are unequal, they are designated by the letters a, b and c. The c-axis is always vertical. The inclined axis is a-axis. It is inclined towards the observer and is also referred as clino axis. The longer horizontal axis is as usual designated as b-axis and runs from right to left. It is also referred as ortho axis. (Fig. 10.32)
The angle between the a-axis and the c-axis is designated as β and is always an acute angle. For the determination of the axial ratio, the length of b-axis is taken as unity.
Normal Class Symmetry:
There are three symmetry classes placed in Monoclinic System.
The symmetry of the normal class (gypsum type) is as given below:
(a) Axis of Symmetry:
1 axis of two fold Symmetry only.
(b) Planes of Symmetry:
1 plane of symmetry only. And a Centre of symmetry. The plane of symmetry is that plane which contains the crystallographic axes ‘a’ and ‘c’.
Forms:
The common forms of this system are:
a. Pinacoids:
A pinacoid is an open form of two faces, each face being parallel to the two axes and cutting the third at a unit length.
Three pinacoids are distinguished in the Monoclinic System:
(i) a-Pinacoid (100):
It is also called orthopinacoid; as the symbol indicates, each face cuts the a-axis and is parallel to the other two axes (Fig. 10.33A).
(ii) b-Pinacoid (010):
It is also called clinopinacoid; in this each face cuts the b-axis at unit length and is parallel to the other two axes.
(iii) c-Pinacoid (001):
It is also called base. The form has two faces, each cutting the vertical axis at unit length.
b. Domes:
A dome is also a form of two faces, each face meeting the vertical axis and one of the other two axes. It is parallel to the third axis (Fig. 10.33).
Two types of domes are recognized depending on to which of the other two axis it is parallel:
(i) Orthodome (hol):
An open form of two faces, each face is parallel to the ortho axis and cuts the other two axis.
(ii) Clinodome (ohl):
An open form of two faces, each face is parallel to the clino axis and cuts the other two axis.
c. Prism:
These are open forms of four faces each, in which each face is essentially parallel to the vertical axis.
There are three types of prisms recognized in the monoclinic system:
(i) Unit Prism (110):
It is an open form of four faces in which each face is cutting the a and b axis at the assumed axial ratio of the species.
(ii) Orthoprism (hko, h>k):
It is an open form of four faces in which each face is parallel to the vertical axis and meets the clino-axis (a-axis) at a greater distance.
(iii) Clinoprism (hko, h<k):
It is an open form of four faces in which each face is parallel to the vertical axis and cuts the ortho axis with a smaller intercept.
d. Pyramids:
These are closed forms and in these each face meets all the three axes. Three types of pyramids are distinguished.
(i) Unit Pyramid (hhl):
Each face cuts all the three axes at the assumed axial ratio of the species.
(ii) Orthopyramid (hkl, h>k):
A type of pyramid in which each face makes a smaller intercept on the orthoaxis. e.g. 321 etc.
(iii) Clino Pyramid (hkl, h<k):
That type of pyramid in which each face makes a smaller intercept on the clinoaxis. e.g. 231 etc.
Examples of Monoclinic Minerals:
(1) Gypsum
(2) Orthoclase
(3) Pyroxene
6. Triclinic System:
Definition:
Those crystals which can be referred to three crystallographic axes, all of which are essentially unequal in length and inclined at various angles to each other, are grouped under triclinic system.
Axial Diagram:
The proper orientation of a crystal of this system would be in which any one of the crystallographic axes is given a vertical position and is designated as c axis. Of the remaining two crystallographic axes, the one which is shorter and sloping towards the observer may be designated as a-axis (brachy axis). The third axis then running approximately right to left and is designated as b-axis (macro-axis). (Fig. 10.35)
Following is the scheme of nomenclature for the angles between the three axes:
α = angle between b axis and c axis;
β = angle between a axis and c axis;
γ = angle between a axis and b axis.
Normal Class:
There are only two symmetry classes falling in the Triclinic System. The normal class is named axinite type after the mineral.
(i) Axes of Symmetry-none.
(ii) Planes of Symmetry-none.
The class is characterized by only a centre of symmetry which is the point of intersection of the three crystallographic axes.
Forms:
All the forms of monoclinic system are found in the crystals of this system also. The main feature of the forms of the triclinic system is that each form has only two faces symmetrical with respect to the centre of symmetry of the crystal. These are, therefore, hemiforms.
a. Pinacoids:
These are open forms, each of two faces, meeting only one axis and being parallel to the other two.
Three types of pinacoids are found in the Triclinic System also as in the Monoclinic and Orthorhombic systems:
(i) a-pinacoid (100) – also called macropinacoid
(ii) b-pinacoid (010) – also called brachypinacoid has two faces each meeting the b-axis at unit length.
(iii) c-pinacoid (001) – also called base has two faces, each intersecting the c-axis.
b. Prisms:
These are open forms of two faces only in the Triclinic System; hence they are also called hemi-prisms. Their general symbol is hko. In all, four prismatic faces with the above symbol are possible, but since there are no planes of symmetry, these four faces will occur in two groups, each being symmetrical to a centre of symmetry only.
c. Domes:
In the Triclinic System, domes are also hemiforms, that is, these contain only one half of the usual number of faces.
The macrodome has two faces, with a symbol of (hol).
The brachydome has two faces with a symbol of (ohl).
d. Pyramids:
Four types of pyramids each with two faces only and each face cutting the vertical axis exist in the Triclinic System. These are called Tetrato-bipyramids (4 bifaced pyramids) represented by the symbol (hkl); Fig. 10.36; 211
Examples of Triclinic Minerals:
i. Albite
ii. Kyanite
iii. Axinite
iv. Microcline
v. Anorthite
vi. Rhodonite
vii. Turquoise