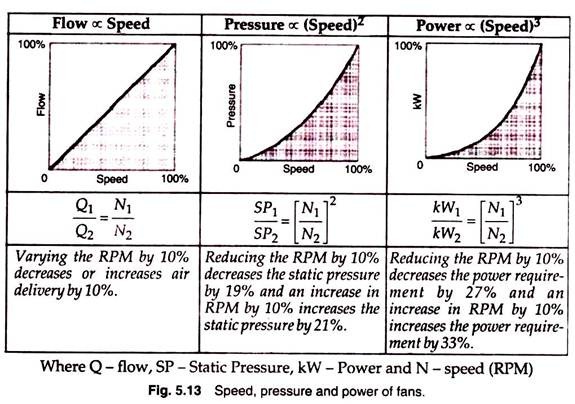
ADVERTISEMENTS:
The non-equilibrium equation can be used to determine the storage coefficient and transmissivity of confined aquifers. These aquifer constants are useful in the design of tubewells and for studying groundwater movement. Several approximate solutions have been developed for the purpose.
Some of them are outlined in the following paragraphs:
1. Theis Method:
This is a graphical method of superposition that makes it possible to obtain solution of Eq. 7.22.
From Eq. 7.22, we can write-
If the discharge Q is held constant, the term in the bracket in Eq. 7.26 and 7.27 are constant, and W(u) is related to u in the manner that s is related to r2/t. Therefore, if the values of s are plotted against r2/t on a logarithmic paper to the same scale as the curve between W(u) and u (known as type curve), the data curve will be similar to the curve except that the two curves will be displaced both vertically and horizontally by the constants shown in Fig. 7.8.
The data curve is super-imposed on the type curve, and a fit, or near fit, is obtained keeping the coordinate axes of the two curves parallel. An arbitrary match point is selected anywhere on the overlapping parts of the two curves, the four values of which (two for each curve) are then used in solving Eqs. 7.23 and 7.25. It is convenient to choose a point whose coordinates on the type curve are both unity, i.e., where W(u) = 1.0 and u =1.0.
Example 1:
An operator starts pumping a 40 cm dia. well at a constant rate. In the first 60 days of pumping drawdown is 3 m. What additional drawdown will be expected if pumping were to be continued for another 60 days at the initial rate? The aquifer consists of sandstone having a porosity of 15%, specific yield 8% and coefficient of permeability 32 m/day. Assume the well fully penetrates a confined aquifer of 42 m thick.
2. Jacob’s Method:
Considering the series solution for the drawdown given by Eq. 7.24, Jacob noted that for small values of r and large values of t, u is small that the terms occurring after the first two terms become negligible. The drawdown can now be written as –
If the values of drawdown are measured at the same time in several wells, these are to be plotted against the logarithm of the respective distances. The graph is known as the distance drawdown graph and Eq. 7.30 is to be used for the value of T.
When the values of the drawdown are measured in one well at various times, the values are plotted against the logarithm of the time and graph is known as the time drawdown graph. Eq. 7.31 is to be used for calculating the values of T.
If the values of drawdown are measured at various times in several wells, the drawdown value is plotted against the logarithm of t/r2 value and Eq. 7.32 is to be used for calculating the values of T. To use these equations, plots are made on a semi-logarithmic graph and value of the change in i for one log cycle is taken. Thus partial derivatives in the above equations can be replaced by s/1.0.
To calculate the value of S, the straight line graph is extended (Fig. 7.11) until it intersects the line zero drawdown. The value of r, t or t/r2 is noted at the point of intersection and the storage coefficient is determined as follows. At zero drawdown-
The use of any of these three formulae depends upon the availability of observations. If only one observation well is available for recording drawdown, time-drawdown method has to be used. Composite drawdown method takes into consideration the data from different wells in different directions and makes it possible to more or less average the data from a single pump test. This method, therefore, is likely to give more realistic values of the aquifer constants.
3. Chow’s Method:
This method developed by Chow does not require any curve fitting. Field observation data is plotted on semilog graph in the same manner as in Jacob’s method (Fig. 7.12). An arbitrary point on the curve is chosen and its coordinates t and s are noted. A tangent is drawn at the selected
point and the value of Δs per log cycle of time is determined. Value of F(u) is calculated using the relation-
For this value of F(u) values of W(u) and u are determined using Fig. 7.12 or Table 7.4. Values of T and S are determined using equations 7.23 and 7.25.
Example 2:
For the same pumping test described in Example Fig. 7.11, calculate the aquifer constants using Jacob’s method.
A plot of s versus t/r2 is made on a semi-logarithmic paper (Fig. 7.11). The line is extended to intersect the t/r2 axis.
Example 3:
A well penetrates a confined aquifer 10 m thick. An observation well is located at 80 m distance from the pumping well. The following observations were made during the pumping operation.
Drawdown in the observation well after 2 hours of pumping = 1.5 m
Drawdown in the observation well after 4 hours of pumping = 2.0 m
Storage coefficient = 0.004.
Calculate the discharge of the well and permeability of aquifer.
Using Jacob’s approximation (Eq. 7.29)-
4. Theis Recovery Method:
If pumping is discontinued in a well, the water level starts rising. The residual drawdown values (the difference between the original drawdown and the rise in water level) could be used for calculating the aquifer constants.
The problem is considered as a recharge well of the same strength as the original well superimposed over the discharging well at any instant. The residual drawdown s’ at any point located at a distance r from the well is obtained using the relationship.
The Drawdown curves during pumping and recovery are shown in Fig 7.13.
The above approach assumes equal values of storage coefficient both before and after pumping. In practice S’ may be smaller than S due to imperfect elastic recovery or air pockets in the aquifer. The recovery data should, therefore, be taken when the storage coefficient S’ is stable after lapse of appreciable time. The straight line given by Eq. 7.37 will pass through the origin only when S = S’.
Example 4:
A fully penetrating well, pumping at a rate of 3 cum/min. was shut down after 4 hours of operation. The residual drawdown was observed in an observation well located at a distance of 20 m from the well. The time-residual drawdown data is given in Table 7.5. Assuming the aquifer to be confined calculate the aquifer constant T.
Solution:
The values of the residual drawdowns are plotted against the corresponding values of t/t’ on a semi-logarithmic graph (Fig. 7.14). Considering one log cycle the value of s’ is obtained as 0.75 metres.
Now using Eq. 7.37-