Stability Analysis of Slope of Earthen Dam: 4 Methods | Geography

An earthen dam usually fails due to sliding of large soil mass from a curved surface. From several investigations, it has been concluded that the sliding of curved surface takes place along its slip surface, which is normally close to the cylindrical shape, i.e. when cross section is in the form of arc.

There have been developed various methods for stability analysis of earth dam. All of them are based on the shearing strength of the soil and certain assumptions with respect to the characteristics of embankment failure.

The most common methods are described as under:

1. Swedish Slip Circle Method:

This method is used to examine the stability of slope of earthen dam. It assumes that the shape of failure plane is in the form of cylindrical arc, and the centre of the possible failure are is known.

In this method to analyse the slope stability, the total earth fill is divided into several vertical segments called slice, which are equally spaced, though it is not necessary. Depending on the accuracy desired, normally six to twelve slices are sufficient. The forces between the slices are considered negligible; and it is also assumed that each slice acts independently as a vertical soil column of unit thickness and width (b). The weight W of each slice acts at its centre point.

Let ‘O’ is the centre, r is the radius of possible slip circle and length of arc DB is divided into 7 slices of equal width (b). The weight of these seven slices are W₁, W₂, W₃…W₇ as shown in Fig. 18.13. The weight (W) has two components; one is normal component (N = W cos α) and other is tangential component (T = W sin α), in which α is the slope angle with the horizontal.

The normal component (N) passes through the centre of the slip circle, i.e. through point (O), hence it does not involve any moment on the slice, but the tangential component (T) causes a disturbing moment, equal to (T. r), where r is the radius of the slip circle. The tangential component of few slices also creates resisting moment, especially when value of T is taken as negative.

If M_d is the total disturbing moment, then it is equal to the algebraic sum of all tangential moments, given as under –

This is the desired expression for calculating the factor of safety against sliding of the earthen dam.

2. Location of Centre of Slip Circle:

Hit and trial method is used to determine the location of centre of slip circle, in which several slip circles are assumed; and factor of safety for each, is calculated. A slip circle which yields lowest value of factor of safety, is considered to be the critical slip circle. For reducing the number of trials, Fellenius has suggested the method for drawing a line (PQ) on which the locus of critical circle is fixed.

The procedure to locate the line PQ for the downstream and upstream slopes of the embank­ment is shown in Fig. 18.14 (a) and 18.14 (b), respectively. The point Q is obtained by taking the co-ordinate as (4.5 H, H) from the toe of the dam, shown in Fig. 18.14.

Similarly, the point P is determined with the help of directional angles (i.e. α₁ and α₂). The values of directional angles α₁ and α₂ for different side slopes are given in Table 18.6.

After determining the position of locus, the critical slip circle is drawn by considering the following points:

1. Critical arc should be passed through the toe of the slope, except for very small value of ɸ.

2. If there exists a hard stratum relatively at a shallow depth under the dam, then the critical arc should not cross this stratum, but can be tangential to it.

3. For very small value of ɸ ranging from 0 to 15°, the critical arc should pass below the toe of the slope; and centre of the critical arc should be on a vertical line drawn through the centre of the slope, as shown in Fig. 18.15.

3. Stability of Downstream Slope during Steady Seepage:

The most critical condition for stabi­lity of downstream slope occurs, when the reservoir is in full condition and the seepage flow is taking place by its maxi­mum rate, because at this condition the seepage flow tends to decrease the stability. In other words, the seeping water below the phreatic line exerts a pore pressure on the soil lying below the saturation line or phreatic line, as result the effective stress acting on the soil mass gets reduce, causing mobilization of the shearing resistance. The factor of safety (FS) for the earth dam under this condition is given as –

In which, ΣU is the algebraic sum of pore pressure acting on the slip circle.

The pore pressure at any point is presented by the piezometric head acting at that point. The variation in pore pressure along the failure arc is obtained by measuring the vertical heights at each of its intersection point with the equipotential line.

Thus, the vertical height measured from the intersection point of equipotential line and the phreatic line is counted as pore water pressure. The pore pressures obtained so are then plotted on a scale in the direction perpendicular to the sliding surface at the respective intersection points, to show the pore pressure distribution along the sliding slope or critical slip surface.

The pore pressure distribution on the critical slip surface is shown in Fig. 18.16 by shaded portion. The area of shaded portion can be measured with the help of planimeter. However, it can also be calculated by using the ordinate method. For example, if Au is the area of U-rectangle and x is the scale of drawing, then total area of pressure diagram (ΣU) can be written as –

ΣU = Au.x² … (18.36)

In absence of flow-net, the following formula can also be used for computing the factor of safety for the downstream slope during steady seepage.

F.S = C.DB + tan ɸ (ΣN’)/ΣT … (18.37)

In this case, the normal components (N’) are calculated by considering the buoyant unit weight (i.e. b. γ_suh . cos α) of the dam, while tangential components are calculated on saturated weight (i.e. γ_sat sin α).

4. Stability of Upstream Slope during Sudden Draw Down:

It is predicted on the basis of horizontal shear force developed at the base of the upstream slope of the dam. However, it is an approximate method, not give exact value.

The basic principle behind this method is that when a horizontal shear force (say P_u) is exerted by the saturated soil then a resistance force opposite to this force (say R_u) is also posed by the soil in the form of shear resistance, which is developed at the base of soil mass, confined within the upstream triangular portion (GMN), as shown in Fig. 18.17.

Where,

W = weight of triangular portion of the dam towards u/s face

C = total cohesive force developed at the base of the dam GN. If ‘C is the unit cohesion of the dam’s soil, then the value of C can be computed by using the equation, C = (Bu. 1).c. In which, B_u is the length of base GN.

The area of triangular portion of upstream slope is indicated by the sum of area GBTN, which is under submerged condition and the area of BMT is under dry condition. The weight W of GMN will be equal to (γ_sub . Area of GBTN + γ_dry . Area of BMT).

The above areas can be obtained by measuring with the help of planimeter. If dry area of u/s face is very less, and entire area is considered to be as submerged, then weight W will get slightly reduced; and thus the values of W tan ɸ, R_u and factor of safety will also be reduced, accordingly. The result obtained by assuming so, makes the u/s slope of dam under safe limit.

Thus, by neglecting the weight of dry area of dam, the net weight W in this case is equal to –

The value of factor of safety against sliding for upstream slope during sudden draw down should be more than 1.5. The calculation of factor of safety by eq (18.42) is done by considering the average shear (S_av), which can be obtained by the following equation –

From studies, it has been found that the maximum intensity of shear force is developed at the distance 0.6 B_u from the heel of the dam in the amount of 1.4 times of average shear stress. The maximum shear stress is given by –

Stability of Upstream and Downstream Slopes during Construction:

When an earth fill dam is constructed with the help of relatively impervious and compressible soils, then there develops excess pore pressure in the newly filled soil mass due to entrapped water and air.

This happening is associated to the reason that the volume of soil mass gets change by compaction of the earth materials at the time of construction. In due course of time the initial pore pressure is gradually dissipated, as a result the shear strength of the soil gets affected. The magnitude of pore pressure developed in the pore space, can be estimated by using the following formula, known as Hilf’s formula –

Where,

U = induced pore pressure.

Δ = compression of embankment, expressed in percent of total original volume of embankment.

P_a = air pressure in pore space of soil mass after initial compaction.

V_a = volume of air in pore space, expressed as percent of original volume of embankment.

h_c = constant, known as Henry’s constant. Its value is taken as 0.02 at 68°F.

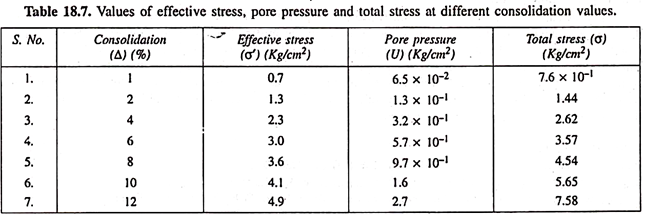
In this method of stability analysis a graph is prepared between the effective stress (σ’) and percentage consolidation, obtained from consolidation test. The values of pore pressure U for various consolidation values are cal­culated from equation (18.47).

By knowing the value of effective stress (σ’) and pore pressure U, the amount of total stress (σ) can be obtai­ned by the relation σ = σ’ + U. An example showing the computation of total stress with the help of σ’ and U, is shown in Table 18.7. The plot between pore pressure and total stress is also shown in Fig. 18.18.

For determining the pore-pressure during construction, the embankment slope is segmented into different parts (i.e. strips), and the mid-height i.e. Z₁, Z₂ … Z_n of each strip is measured; and stress is estimated for each of them and lastly they are added together to get total stress (σ). Using Fig. 18.18, the corresponding values of U for various values of stress are determined.

ΣU = (U) x Width of slice

In other way, by taking the values of U from Table 18.7, the distribution curve is prepared for the slip circle, and the value of ΣU is obtained by knowing the area (A_u).

After knowing the value of ΣU, the factor of safety (F.S.) to predict the stability of upstream and downstream slopes, when reservoir’s water gets suddenly down, can be calculated by using the formula.