ADVERTISEMENTS:
Analog models physically simulate the field prototype condition either by using actual aquifer materials for direct representation or by indirectly simulating the aquifer and flow by various physical analogies, such that the partial differential equations that describe the response of the two system, i.e., prototype and analog model, are similar.
Analog models applicable to ground water problems are of two types:
(a) Mechanical analogs, and
ADVERTISEMENTS:
(b) Electric analogs.
(i) Sand Models in Glass Flumes:
There have long been used for the solution of seepage problems and will provide useful information. They involve the application of Darcy’s law and the equation for simulation of the model is-
Qr = KrirLr2 …(6.1)
ADVERTISEMENTS:
Where r = subscript for the model-prototype ratio; Lr = length ratio and Lr2 = area ratio.
(ii) Viscous Flow Model (Parallel Plate of Hale-Shaw Model):
The viscous flow of liquid between closely spaced parallel plates simulates two-dimensional ground water movement. The viscous flow model consists of two closely spaced parallel glass plates or transparent Perspex sheets with a capillary space of constant width of 1 to 1.5 mm and viscosity of the fluid, such as glycerine, appropriate to the permeability of the aquifer.
ADVERTISEMENTS:
The loss of head between two closely spaced parallel plates is given by Poiseuille’s equation-
Where h – loss of head; µ = dynamic viscosity of the liquid; γ = specific weight of the model fluid (= ρg); B = space between parallel plates; L = length of the plates and v = velocity of flow of the model fluid.
Putting B = 2a in Eq. (6.2)-
Where V (= µ/ρ) = kinematic viscosity of the model fluid; ρ = density of the model fluid and Km (= a2g/3v) = model permeability.
Eq. (6.3) is analogous to Darcy’s law-
v = Ki
The velocity ratio between model and prototype-
Where k (=cd2) = coefficient of intrinsic or physical permeability depending on soil characteristics alone and µ, γ = viscosity and specific weight of water in the field, respectively-
Where r = subscript for model-prototype ratio and Lr = linear scale ratio.
The plate spacing and fluid can be selected to correspond to a desired permeability. The model may be of horizontal or vertical type, but the latter has greater application. It can represent two phase flow by using liquids of different density. This makes the viscous flow model ideal for simulation of conditions involving fresh and saline waters and prediction of the interface movement under changing conditions of abstraction and replenishment.
The water table or piezometric levels in wells can be observed in the vertical model and the flow lines can be seen and photographed if dye is added to the viscous liquid. Storage is simulated by the addition of small storage reservoirs connected to the interspace. The parallel plate model is isotropic with respect to permeability; but local variations in width of the interspace may be made by placing obstructions between the plates to simulate non-homogeneity. The liquid used may be water with some substance added to increase its viscosity, glycerin or any petroleum oil.
(b) Electric Analog Models:
Various models such as conductive paper (teledeltos) and electrolytic tanks make use of the analogy between the subsoil flow (Darcy’s law) and flow of electricity (Ohm’s law) but to a large extent they have been superceded by networks consisting of a mesh of resistors linked together at nodal points to give a square, rhombic or polygonal pattern. Currents may be fed into the mesh in accordance with the predetermined inputs of infiltration and leakage or may be led out of the mesh as simulation of well abstraction or effluent flow to rivers.
RC Network Analog:
Further refinement is made by adding to the resistor mesh, at nodal points, grounded capacitors which represent the coefficient of storage in the aquifer. Recharge boundaries are simulated by common connections and impermeable boundaries by open ends. Each node in RC (resistor- capacitor) network analog represents a location for a well. Pumping at a constant rate at any well is simulated by injecting a negative current pulse of scaled duration at the corresponding node in the analog.
The transient response of all other nodes is studied by observing their varying potentials with the help of a cathode ray oscilloscope. These transients represent the time-drawdown characteristics of the aquifer at the corresponding locations. The electrical analog is then modified step by step in its values of resistors and capacitors, such that all observed drawdown histories in the wells for the corresponding causative pumpages are correctly simulated by the electrical transients at the corresponding nodes.
If this step by step modification is done completely and satisfactorily; then the analog can be relied upon to compute any drawdown at defined locations and times, for given excitations of the aquifer. However, this modification process is invariably very arduous and frustrating and perfect simulation of the aquifer is very difficult to achieve.
The aquifer is subdivided into squares of equal area ∆x ∆γ. A resistor-capacitor network with a square pattern as shown in Fig. 6.1 (a) and network junctions at nodes as defined in Fig. 6.1 (b) is set up. The intersections of grid lines are called nodes. The junctions consists of 4 resistors and 1 capacitor connected to a common terminal; the capacitor is also connected to the ground. The infinitesimal ∆x ∆ γ = ag2, in which ag is the width of the grid interval.
The area ag2 is small compared to the size of the model (representing the entire aquifer) and the behaviour of the discontinuous network closely simulates the continuous aquifer. Because the model consists of discrete elements, a finite difference form of the partial differential equation for the unsteady ground water flow is used for comparison with the equation for the flow of electric current. The finite difference form of the partial differential equation [Eq. (6.8)] is-
Where h1 is the head at node 1 and hi the heads at nodes 2-5.
The relation of electrical potentials in the vicinity of the junction, according to Kirchoff’s current law, can be expressed as-
Where Vi, V1 = the electrical potentials at the ends of resistors 2-5 and 1, respectively; R = resistance and C = capacitance.
From Eqs. (6.10) and (6.11), the analogy between electrical system and aquifer system is apparent and by inspection of the two equations, the analogous parameters in the two systems are-
Scaling factors are necessary to provide for proportionality of the analogous parameters in the two systems. To illustrate this, consider an aquifer of 6 × 4 km extent and of uniform thickness of 50 m, with a permeability of 3m/day and S = 10-3. The aquifer may be assumed under uniform pressure at every point. The aquifer can be divided into a number of equal blocks, the size of each block being determined on a compromise between economy and accuracy required. Let the aquifer be divided into 24 blocks each of 1 km × 1 km × 50 m size. If a differential head of 1 m is maintained between the faces of any block, the flow will be-
The electrical equivalent to each block will be a network of four resistors each of 1/4 megoham and one capacitor of 0.0067 microfarad, meeting a one common node, with the other end usually earthed. Each node is connected to its neighbour through the resistors.
The analogue is constructed on a peg board on which is placed on a map of the area. The map usually shows transmissibility in addition to physical features such as roads and towns. A square grid matching the holes in the peg board is overlaid on the map by attaching four resistors to the peg. The capacitor for that node is usually placed on the reverse side of the board. A typical R.C. network is shown in Fig. 6.1.
Leakage can be simulated in the analogue model by the addition of resistors connected to ground and to each node of the network, Fig. 6.1(c). Barrier boundaries can be simulated by an open circuit. Resistors connected to the nodes along the edge of the analogue model and to the ground, simulate horizontal leakage through boundaries of the aquifer. Leakage of water through a stream bed can be simulated with a resistor connected to appropriate nodes and to ground.
To the resultant RC mesh are applied transient currents of ‘square form’ type from a pulse generator and the resultant voltage response is observed on an oscilloscope, Fig. 6.2, or traced by a x-y plotter, depending on whether ‘fast time’ or ‘slow-time’ equipment is available. Once the model is verified, i.e., faithfully produces historically observed trends after adjustments, it is possible to vary the duration and rate of pumping, or of influence seepage from natural or artificial sources, and observe the resultant change of voltage (water level in the aquifer) with time at any point within the mesh. The excitation-response apparatus is comprised of four major parts: a power supply, a wave form generator, a pulse generator, and an oscilloscope.
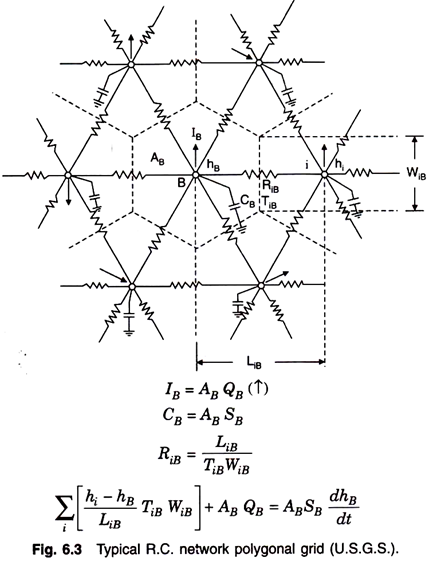
The RC model is the most versatile and is finding great utility in long term prediction of effects of pumpage on ground water levels and on stream flow. The USGS uses many thousands of nodes to represent a ground water basin. A typical resistor-capacitor network polygonal (non-square) grid used by USGS is shown in Fig. 6.3.
A case history of an R.C. network analog model constructed to determine the effects of continued pumping of ground water from the unconfined aquifer of Pochampad Ayacut in Andhra Pradesh is given below:
(i) Area of Ayacut modelled = 67 km2. The wedge shaped area (quite fertile and productive) is bounded on the two sides by Peddavagu and Koratlavagu and on the third side by the Pochampad main canal.
(ii) Ground water in this basin is mostly under unconfined conditions in the weathered zone of the formations. Pump tests in a few representative open wells were conducted and the data was analysed by Papadopulos and Cooper method and the average values of the formation constants were obtained as T = 79.5 m2/day and S = 4.55 × 10-3.
(iii) The area was divided into a network of square grids of size 1 km × 1 km as shown in Fig. 6.4, which resulted in 91 nodal points.
(iv) Scale factors were arrived as follows:
(a) Internal resistor of the analog model-
R = 10 kΩ
Therefore, R = 1/T, 104 Ω = 1/79.5 m2/day
1Ω = 1/79.5 × 103 day/m2
(b) The water table contours of Jan. 1971 as shown in Fig. 6.5 indicated that the maximum and minimum water table elevations were at 304 and 270, respectively giving a head difference of 34 m. Hence, a scale of hydraulic head (h) was adopted as-
1 m = 1 V
For preliminary studies the values of the boundary resistors and capacitors were kept same as those of internal ones. A calibrating resistor Ri = 4.7 kΩ was used for simulating pumping rate, Fig. 6.6. For example, for a pumping rate of Q – 1.69 × 102 m3/day, I = 1.69 × 102/7.95 × 105 = 0.213 × 10-3 amp and the excitation voltage across the calibrating resistor VR =V1-V2 = I × Rt = (0.213 × 10-3) × (4.7 × 1000) = 1 volt, when a pulse was sent to the pumping well junction or node P1; the response (i.e. trace of the voltage drop against time) at an observation node O1 due to the excitation at the pumping node P1, was observed on the oscilloscope screen from which the corresponding time-drawdown relationship was obtained.
(v) Calibration of the Analog Model:
At each node, a solder lug was bolted which served as a common terminal for four resistors and one capacitor. All the capacitors were grounded to the common earth grid. The two streams were simulated as recharge boundaries by terminating the portions of the network along the boundaries in short circuits. Since the Pochampad main canal was excavated beyond the average depth of weathering in the region and as the canal is also lined, it was assumed that there was no under flow. The boundary was simulated as a barrier boundary with no flow across it by an open circuit.
Taking the confluence of the two at node 91 as the datum, a potential difference of 34 V between the nodes 91 and 1, and a potential difference of 32 V between nodes 91 and 32 were maintained and the resulting pattern of declines in potential across the various nodes were measured and transformed into hydraulic potentials. Fig. 6.5 shows the initial water level elevations as observed on the analog model and the actual water table levels collected from field data.
(vi) Experimental Set-Up and Operations of the Analog Model:
The excitation response apparatus consisted of a pulse generator, power supplies and an oscilloscope (Fig. 6.6 and 6.7). The pulse generator generated pulses at regular intervals of time and by adjusting the amplitude and width of the pulse, the required pumping rate could be simulated. To simulate the boundary conditions, a transistorised regulated twin power supply was used.
An oscilloscope was used to measure the response at the observation well to the different pumping rates at the pumped wells. Four arbitrary nodes were chosen as pumping centres with pumping rates of 1.69 × 102 m3/day (at nodes 7 and 9) and 3.38 × 102 m3/day (at nodes 20 and 76). If one observation well was influenced by more than one pumping centre, the values were algebraically added.
One of the pumping, nodes was first, excited with an assigned value of discharge and the effect (i.e., the response as voltage vs. time which gave the time-drawdown curve to a different scale) at any other node was observed on the oscilloscope as shown in Fig. 6.8.
Time- drawdown curves at various observation nodes due to the two different rates of pumping at node 20 are shown in Fig. 6.9.
The predicted pattern of water table contours at the end of 1, 5 and 10 years when the four pumping centres were pumped simultaneously with different pumping rates are shown in Fig. 6.10. There was a maximum decline of 15 m head along the Pochampad main canal and of about 5 m at the confluence of the two streams. A marked shift in the contours was observed for a pumping period of 1 year and very little shift for 5 and 10 years.
(vii) Conclusion:
Thus, analog model can be used for examining the various choices of ground water development and to plan spacing of wells.
Scale Factors for R.C. Network Analog:
The following scale factors were defined for R.C. network analog models:
Vertical flow between aquifer layers can be simulated through resistor Rv connecting two or more resistance networks, Fig. 6.6. Values of Rv can be obtained from-
Where b’ = vertical nodal spacing or the distance between layers, and K’ = coefficient of vertical permeability.
Irregular shapes of boundary are duplicated by ‘vector volume technique’. The values of the resistors and capacitors adjacent to boundaries can be computed from the ‘vector volume’ technique described by Karplus (1958) as-
Where Rx = value of the x-direction resistor adjacent to a boundary; Ry = value of the y-direction resistor adjacent to a boundary; Rb = value of resistors in interior portions of the model and ∆x, ∆y = length of the aquifer represented by the resistors in x and y directions, respectively.
The magnitudes of capacitors are directly proportional to the areas of the portions of the aquifer they represent. The value of the capacitor adjacent to a boundary is given by-
Where Av = area of the aquifer represented by the capacitor.
R.C. Analog with Continuous Resistance Medium:
A method has been developed using continuous resistance medium of suitable liquids to represent the hydraulic resistance of the aquifer, discrete capacitors being used at designed locations. The continuity of the liquid resistor ensures better simulation.
Assuming the scales-
Where ρ = resistivity of the medium (analog liquid), ohm-cm; K = permeability of the aquifer, m/day, and S = storage coefficient of the aquifer, fraction.
The frequency and duration of current pulses can be adjusted for given pumping durations by time scaling as given above. Simultaneous injection of pulses of different magnitudes and phase relationships to each other is possible with independent pulse generators isolated from each other. The response as transients are photographed for further analysis.
New Type of Direct Simulation Analog:
A circular tank 80 cm in diameter with an insulating boundary contains an electrolyte about 10 cm deep. A number of copper rods of various diameters (6-20 mm) penetrating the electrolyte to various depths at different locations form the nodes of the electrical network. The electrolytic medium is the continuous resistance field. To each probe (called penetrode) is connected a variable capacitor to simulate storage effects.
By varying the diameter, position and penetration of each penetrode, it has been found possible to create a network which should be a scaled version of any other given network of discrete resistors and capacitors. Simulation of the aquifer is complete when the excitation-response pairs are reproduced exactly at homologous points. The only data used are the histories of pump excitations and aquifer responses and no data relating to hypothetically derived parameters such as S and T, will be necessary.
Dipole Pumping Test:
Two wells drilled near each other, say within about 10 m, constitute the dipole, with both wells connected at the top by a pressure pipe connection. Water pumped out of the aquifer from one well is used to recharge the aquifer through the other well. The pressure differential which causes flow in the dipole-aquifer circuit (Fig. 6.11) and the corresponding flow rate are measured continuously. Steady state conditions are obtained in comparatively short time.
The same number of dipoles as in the aquifer are employed in the analog model. The pattern of excitation-response pairs are simulated in its transformed and scaled version by manually operating to vary the locations and penetrations of the limbs (penetrodes) of the analog dipoles. All the hydrologic characteristics of the aquifer are reflected in the excitation- response pair at each dipole in the aquifer.
It is also possible to transduce the pressure differential flow pair signals from the aquifer dipoles into voltage difference current pairs, and telemetrically feed the servos of the analog model to operate the dipole limbs. Prediction of any required response can be done by exciting the model in the required manner and observing the responses at topologically corresponding points in the model tank, and then interpreting the results in terms of the aquifer parameters.
In a more sophisticated version of this technique electrical dipoles are excited electrically by injecting a square wave current pulse across them. The transient responses (in the form of time-varying electrical potentials) of a number of electrodes buried in the aquifer, Fig. 6.11 are telemetered to the model tank, in addition to the transmission of the scaled excitation pulses also. Thus the analog tank receives a number of electrical excitation-response pairs from all the dipoles and electrodes buried in the aquifer. Quick acting servos by automatically operating the analog dipoles, capacitors and electrodes create a homologous R.C. net simulating the aquifer at every instant.
This analog model, after linking with a suitably programmed digital computer can be used to transmit commands to the aquifer pump for regulating their pumping rates and durations, satisfying any criteria (such as limiting drawdowns in a number of wells) that may be stipulated for the economic exploitation of the aquifer. Depending upon the instantaneous aquifer parameters and recharge conditions, and constrained by the policy criteria set up for the aquifer, automatic regulation of pumping in an aquifer can be achieved.
Numerical Solution:
Substituting in the Laplace equation-
Which is in the finite difference form. The finite-difference solution of the Laplace equation thus states that ‘h’ at each node must be equal to the average of h at the four surrounding nodes. The difference-
The procedure for finding the correct value of head at each node is to:
(i) Define the boundary conditions by assigning proper ‘h’ values and assign tentative values of h for the rest of the nodes of the chosen grid.
(ii) Determine the residual at each node as per Eq. (6.22)
(iii) Apply corrections to the assumed values to reduce the residuals to some small value.
(iv) After reducing re, at a particular node to minimum and altering h0, alter the residuals of adjacent nodes by the change in h0. For an impervious boundary ∂ф/∂n = 0, since the velocity normal to the boundary must be zero.
For a vertical impervious boundary-
After determining the correct values of h at each node, equipotential can be drawn (by interpolation) and streamlines drawn as orthogonal, to form a flownet, from which the flow rates can be determined. If the boundaries of the area constitute streamlines, time may be saved by solving the flow system in terms of ѱ (instead of h) and drawing the equipotential as orthogonal to the streamlines.
Special techniques have been developed to most efficiently ‘relax’ the system from its residuals, hence the name relaxation method. Manual operation of the relaxation method is time consuming. The work can be shortened by using ‘block relaxation’. The accuracy of the relaxation method depends on the density of the network (typically 50 to 200 nodes).
The method can also be applied to heterogeneous medium with irregular boundaries or axisymmetric systems. In areas where the flow is concentrated subdivided networks may be used to produce greater node density. Automatic relaxation can be obtained through iteration by digital computers. The manual relaxation method has been superseded by R.C. network analog and digital computers.
If the thickness of the aquifer and its permeability is known, the hydraulic gradient, seepage velocity and flow rate across any section of the aquifer can be estimated.
Example 3:
A line of wells equally spaced at 1.2 km is located between a stream and barrier boundary, which are parallel and 1 km apart. The line of wells is at 0.6 km from the stream. The transmissibility of the aquifer may be assumed as 160 m2/day. When the wells are pumped, the water level in the wells is about 6 m below the stream. Determine the water table elevations and flow into the wells by drawing a flow net.
Solution:
Due to symmetry, the flow system will be a repetition of the pattern in the rectangle ABCD Fig. 6.13. BC, CD, and AD are streamlines. AB is an equipotential and is assigned values of 100; the pumping well W is assigned a value 0. The h-values within the area are evaluated for a 6 × 10 grid by relaxation method performing a few iterations, and the final levels (along with the minimum residuals towards left carrying ± sign) are given in Fig. 6.14. The equipotential lines are drawn by interpolation, streamlines sketched as orthogonals to the equipotentials, and a flownet is thus obtained.
For a homogeneous, isotropic aquifer infinite in areal extent, with co-efficient of storage S and transmissibility T, with a steady rate of recharge P, the differential equation for two- dimensional flow is-
Where ∆h0 is the change in head at node ‘0’ during the time interval ∆t.
The head distribution in time and space in an aquifer of given size and slope can be found by relaxation or interaction method.
The differential equation for two-dimensional flow in a nonhomogeneous aquifer infinite in areal extent with a steady rate of recharge P is-
It is assumed that all parameters vary in space and P varies both in space and time.
The entire aquifer can be divided into a network of square, triangular, or hexagonal grids which are so small that the variation of head can be taken to be linear, Fig. 6.15.
Considering the hexagonal area of a triangular net (shaded area); flow through one side of length l (a/√3), Fig. 6.16.
By adding the flow through all the six sides, the total flow leaving the shaded hexagon (6.26a)-
If there is no recharge the total flow leaving the shaded prisms would be zero, when-
Which states that the head ‘h’ at any node must be equal to the average of h at the six surrounding nodes. This can also be obtained by the method of finite differences.
As an example, for an aquifer, bounded by two streams as shown in Fig. 6.17, the water levels in the rivers and in the observation wells at the upstream boundary of the aquifer are given. The distribution of water levels or piezometric heads can be obtained by fitting a triangular network and assuming linear variation between the two given values of heads. The aquifer boundaries are slightly deformed to adjust for the straight sides of the triangles.
Tentative values of heads are assumed at the interior nodes and then altered, such that the residuals (i.e., the difference between the assigned value and the average of the six surrounding values) are reduced to a minimum. From the final value of heads at the nodes (arrived after two-three iterations), the equipotential lines can be drawn, and the flow lines sketched orthogonal to the equipotential lines to obtain the flownet, Fig. 6.18, from which the flow velocities and flow rates across any section of the aquifer can be determined.
In ground water flow problems, triangular nets are preferred, since the shaded hexagon approaches a circular shape which compares with radial flow problems.
If there is a uniform steady recharge P over the area of the shaded hexagon ((√3/2 )a2), then the Eq. (6.27) becomes-
In case of semi-confined aquifers with piezometric head ‘h‘’ the flow rate into the shaded area is-
Variable Thickness in Unconfined Aquifer:
In unconfined aquifers the saturated thickness is not a constant and this variation in thickness has to be taken into account. In Eq. (6.26c)
If there is a uniform recharge P over the shaded area √3/a (a2)-
When there are pumping wells in the area, the drawdown due to each well can be determined from the steady state logarithmic formula. This should be subtracted from the results obtained by numerical analysis.